01背包问题指的是有n个物体，有自己的重量和价值，放到一个容积为j的背包中，求它们最多能放进那几个物品让有固定体积的背包里面的价值最大，与完全背包不同的是每个物品只能选择一次

关于DP数组

DP是 dynamic programming 的缩写，一般用来解决类似动态规划问题的一个数组，可为一维数组或者多维

定义dp[i][j]

这里表示[0,i]个物品被放置到质量为j的背包中的最大价值

其中他只有两个状态

• 不放当前物品
  dp[i][j] = dp[i-1][j]

（此时对应的背包价值是dpi-1,因为你不放物品i。背包对应的肯定是[0,i-1]的物品中的最大值）

• 放当前物品

dp[i][j] = dp[i-1][j-weight[i]] + value[i]

weight[i]指的是当前i的重量
value[i]指的是当前i的价值
（此时对应的背包价值是dpi-1]+value[i]）

递推公式

dp[i][j] = Math.max( dp[i-1][j-weight[i]] + value[i],dp[i-1][j])

初始化，确定base

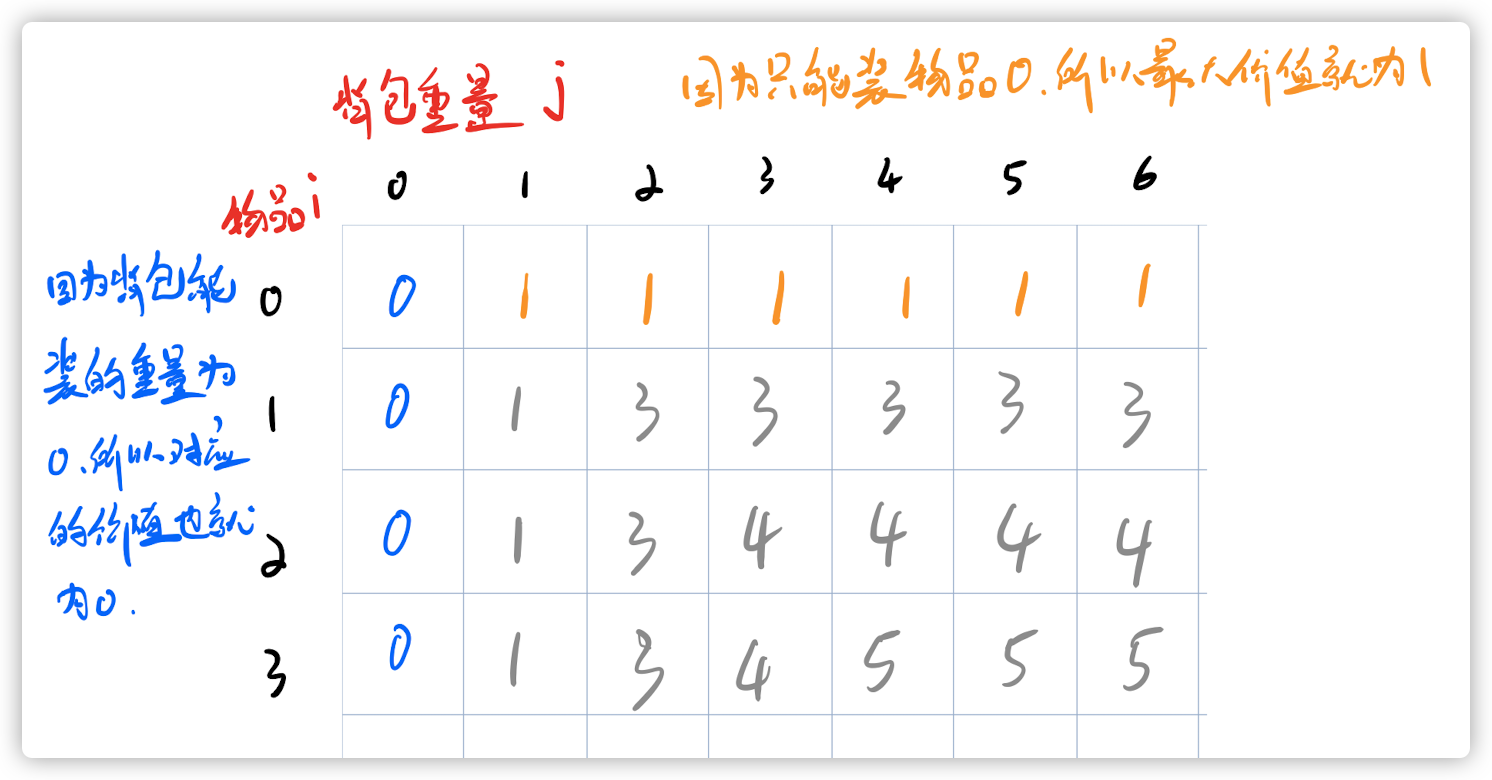
1. 因为背包容量是0，对应的价值肯定也是0
2. 因为不管体积是多少，也只能装物品编号为0的物品，所以对应的重量为1

确定递推公式

// 对于二维数组来说，这里面的可以随意更改for循环的先后顺序
for(i=1,i<物品个数+1,i++){
    for(j=1,j<背包总重量，j++){
        dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-物品i的质量]+物品i的价值)
    }
}

递推结果